Professor of Mathematics
Contact
Publications
Programs
Talks
Teaching
Service
Recreational
News
3 November 2025: Schläfli
lecture by Kathlén Kohn.
Recreational Mathematics
The Casas-Alvero conjecture
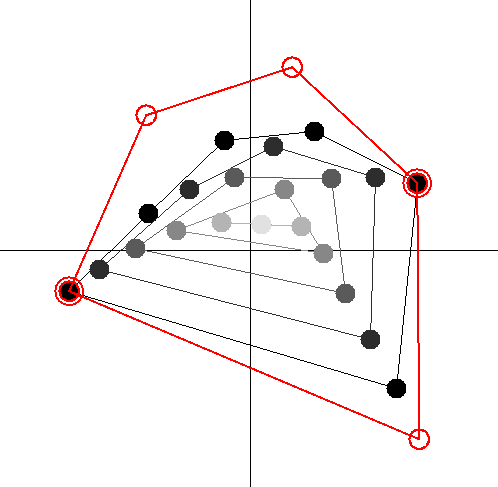
The Casas-Alvero conjecture states that a univariate, complex polynomial f of positive degree n that has a non-trivial gcd (i.e., a root in common) with each of its derivatives f', f'', ..., f(n-1) must be of the form a(x-b)n. The conjecture is known to hold if n=q pe with q in {1,2,3,4} and p a prime larger than q, except possibly for q=4 and p=7. For q=1,2 this is proved here, and for q=3,4 the statement can be proved in a similar fashion. Clicking on the picture below opens an applet, written by my Bachelor student Johan P. de Jong, with which you can get a feeling for why the conjecture might be true---if you try to make roots of f coincide with roots of its derivatives, then the roots seem to have the tendency to "collapse" into a single point. Left-clicking adds a root or increases the multiplicity of an existing root, right-clicking deletes a root or decreases the multiplicity of an existing root, and the roots of derivatives of f are depicted in ever lighter shades of grey. The applet uses Michael Thomas Flanagan's Java library for complex polynomials.
Tree chomp
Chomp is a game that can be played on any partially ordered set with a a smallest element. Two players alternatingly remove an element of the set, together with all larger elements. The player who is forced to remove the minimum loses the game. Classical chomp is played on a chocolate bar, and very hard to analyse. See this page for mathematics and links and an applet. Another special of chomp case is graph chomp. A yet more special case, which should be analysable by good high school students, is tree chomp, for which I wrote an applet once. S/he who takes the last vertex wins the game; can you find a strategy?A poem about mathematics
ArrowsA mathematician's most common mistake
takes products to sums, and sub-things to quotients;
semisimplicity can only fake
the lurking, neglected emotions.
But don't despair!
A one-way road back is there, though narrow:
immediate re-reversal of the arrow.